-
Adam Rhodes
Authors:
Adam Rhodes, Department of Mathematical and Statistical Science, University of Alberta
Prof. Thomas Hillen, Department of Mathematical and Statistical Science, University of Alberta
Accumulating experimental and clinical evidence suggest that the immune response to cancer is not exclusively anti-tumor. Indeed, the pro-tumor roles of the immune system — as suppliers of growth and pro-angiogenic factors or defenses against cytotoxic immune attacks, for example — have been long appreciated, but relatively few theoretical works have considered their effects. Inspired by the recently roposed “immune-mediated� theory of metastasis, we develop a mathematical model for tumor-immune interactions in the metastatic setting, which includes both anti- and pro-tumor immune effects, and the experimentally observed tumor-induced phenotypic plasticity of immune cells (tumor “education� of the immune cells). Upon confrontation of our model to experimental data, we use it to evaluate the implications of the immune-mediated theory of metastasis. We find that tumor education of immune cells may explain the relatively poor performance of immunotherapies, and that many metastatic phenomena, including metastatic blow-up, dormancy, and metastasis to sites of injury, can also be explained by the immune-mediated theory of metastasis. Our results suggest that further work is warranted to fully elucidate the pro-tumor effects of the immune system in metastatic cancer.
-
Ruby Kim
The superchiasmatic nucleus (SCN) serves as the primary circadian (24hr) clock in mammals, and is known to control important physiological functions such as the sleep-wake cycle, hormonal rhythms, and neurotransmitter regulation. Experimental results suggest that some of these functions reciprocally influence circadian rhythms, creating a complex and highly homeostatic network. Among the clock's downstream products, orphan nuclear receptors REV-ERB and ROR are particularly interesting because they coordinately modulate the core clock circuitry. Recent experimental evidence shows that REV-ERB and ROR are not only crucial for lipid metabolism, but are also involved in dopamine (DA) synthesis and degradation, which could have meaningful clinical implications for conditions such as Parkinson's disease and mood disorders.
We create a mathematical model that includes the circadian clock, REV-ERB and ROR and their feedback to the clock, and the influences of REV-ERB, ROR, and BMAL1-CLOCK on the dopaminergic system. We compare our model predictions to experimental data on clock components in different light-dark conditions and in the presence of genetic perturbations. Our model results are consistent with experimental results on REV-ERB and ROR and allow us to predict circadian oscillations in extracellular dopamine and homovanillic acid that correspond well with observations.
The predictions of the mathematical model are consistent with a wide variety of experimental observations. Our calculations show that the mechanisms proposed by experimentalists by which REV-ERB, ROR, and BMAL1-CLOCK influence the DA system are sufficient to explain the circadian oscillations observed in dopaminergic variables. Our mathematical model can be used for further investigations of the effects of the mammalian circadian clock on the dopaminergic system. RR{The model can be used to predict how perturbations in the circadian clock disrupt the dopamine system and could potentially be used to find drug targets that ameliorate these disruptions.
-
Paul Hurtado
The Linear Chain Trick (LCT) has long been used to build ODE models (specifically, mean field state transition models) by replacing the implicit assumption of exponentially distributed passage times through each state with more "hump shaped" gamma (or more specifically, Erlang) distributions. Recently, we introduced a Generalized Linear Chain Trick (GLCT) where we showed that there was a straightforward way of writing down mean field ODEs for a much broader family of assumed "dwell-time" distributions known as the Phase-type distributions. These are essentially the hitting-time or absorbing-time distributions for Continuous Time Markov Chains (CTMCs), and include Erlang, Hypoexponential, Coxian, and related distributions. Methods for fitting these matrix exponential distributions to data have been developed for applications of queuing theory, allowing for more flexibility than just incorporating best-fit Gamma distributions into ODE model assumptions. In this presentation, I will illustrate how the SEIR model can be extended using the LCT and the GLCT, and how the structure of the resulting model, when viewed through the lens of the GLCT, can be leveraged in subsequent analytical and computational analyses.
-
Jinsu Kim
In cellular immune responses, inflammatory ligands activate signal-dependent transcription factors (SDTFs), which can display complex temporal profiles. SDTFs are central effectors for inflammatory gene expression. However, the information contained in SDTF signals must also be decoded by the epigenome in a stimulus-specific manner, to allow controlled plasticity in cellular epigenetic states in response to environmental encounters. The mechanisms and biophysical principles that generate distinct epigenomes in response to different SDTF signaling remain unclear. Here, we develop and analyze stochastic models of nucleosome accessibility to study how SDTF signals alter the epigenome dynamics. Interestingly the response of our epigenome model to SDTF signals helps us to predict the cooperativity of genome-scale nucleosome in vivo. Two alternative but reasonable hypotheses on the cooperativity of parameters in nucleosome unwrapping steps were experimentally tested by ATAC sequencing. On the genome-scale, the location of SDTF binding is a predictor of nucleosome accessibility since the epigenome dynamics depends on SDTF binding sites differently under cooperative and non-cooperative parameters. We could compare our numerical results to experimental measurements to test our prediction. Our work proposes a framework that allows a predictive understanding of how nucleosomes respond to SDTF signaling at specific genomic locations to produce chromatin alterations in health and disease conditions.
-
Marissa Renardy
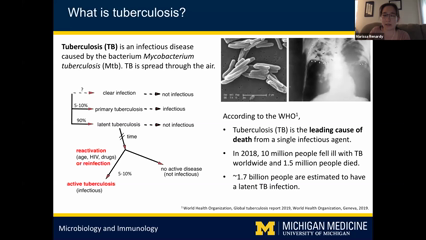
Mycobacterium tuberculosis (Mtb), the causative agent of tuberculosis (TB), kills more individuals worldwide per year than any other infectious agent. As the hallmark of TB, lung granulomas are complex structures composed of immune cells that interact with and surround bacteria, infected cells, and a necrotic core. This interaction leads to diverse granuloma outcomes across time, ranging from bacterial sterilization to uncontrolled bacterial growth, as well as diverse spatial structures. Currently, there are no systematic quantitative methods to classify the formation, function, and spatial characteristics of granulomas. This type of analysis would enable better understanding and prediction of granuloma behaviors that have known associations with poor clinical outcomes for TB patients. Herein, we develop a temporal and spatial analysis framework for TB granulomas using a systems biology approach combining in silico granuloma modeling, geographic information systems, topological data analysis, and machine learning. We apply this framework to simulated granulomas to understand temporal granuloma dynamics, quantify granuloma spatial structure, and predict the relationship between granuloma structure and bacterial growth. As a proof-of-concept, we apply our in silico predictions to in vivo derived data to test our framework for future applications and as a personalized medicine intervention.
-
Padi Fuster Aguilera
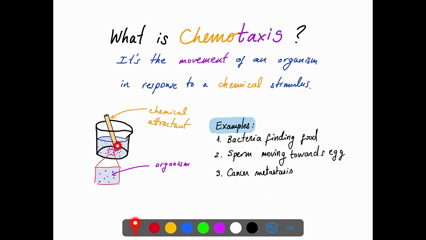
We study a particular model derived from a chemotaxis model with logarithmic sensitivity and logistic growth. We obtain existence and uniqueness of solutions as well as results for the limit diffusion of the solutions with Neumann boundary conditions.
-
Suzanne Robertson
Outbreaks of vector-borne diseases such as Zika virus can occur after an infected individual introduces the virus to a residential neighborhood after traveling. Management strategies for controlling vector-borne disease typically involve large-scale application of larvicide or adulticide by truck or plane, as well as door-to-door control efforts that require obtaining permission to access private property. The efficacy of the latter efforts depend highly on the compliance of local residents. We present a model for vector-borne disease transmission in a neighborhood, considering a network of houses connected via mosquito dispersal. We use this model to compare the effectiveness of various control strategies and determine how optimal use of door-to-door control and aerial spraying depends on the level of resident compliance as well as mosquito movement. This is joint work with Jeffery Demers, Sharon Bewick, Folashade Agusto, Kevin Caillouet, and Bill Fagan.
-
Deena Schmidt
Classical contagion models, such as SIR, and other infectious disease models typically assume a well-mixed contact process. This may be unrealistic for infectious disease spread where the contact structure changes due to individuals' responses to the infectious disease. For instance, individuals showing symptoms might isolate themselves, or individuals that are aware of an ongoing epidemic in the population might reduce or change their contacts. Here we investigate contagion dynamics in an adaptive network context, meaning that the contact network is changing over time due to individuals responding to an infectious disease in the population. We consider norovirus as a specific example and investigate questions related to disease dynamics and applications to public health.
-
Bismark Oduro
Chagas disease is a major health problem in rural South and Central America where an estimated 8 to 11 million people are infected. It is a vector-borne disease caused by the parasite Trypanosoma cruzi, which is transmitted to humans mainly through the bite of insect vectors from several species of so-called kissing bugs. One of the control measures to reduce the spread of the disease is insecticide spraying of housing units to prevent infestation by the vectors. However, re-infestation of units by vectors has been shown to occur as early as four to six months after insecticide-based control interventions. I will present ordinary differential
equation models of type SIRS that shed light on long-term cost effectiveness of certain strategies for controlling re-infestation by vectors. The results show that an initially very high spraying rate may push the system into a region of the state space with low endemic levels of infestation that can be maintained in the long run at relatively moderate cost.
-
Wasiur KhudaBukhsh
Motivated by the classical Susceptible-Infected-Recovered (SIR) epidemic models proposed by Kermack and Mckendrick, we consider a class of stochastic compartmental dynamical systems with a notion of partial ordering among the compartments. We call such systems uni-directional Mass Transfer Models (MTMs). We show that there is a natural way of interpreting a uni-directional MTM as a Survival Dynamical System (SDS) that is described in terms of survival functions instead of population counts. This SDS interpretation allows us to employ tools from survival analysis to address various issues with data collection and statistical inference of unidirectional MTMs. We use the SIR model as a running example to illustrate the ideas. We also discuss several possible generalizations of the method.
-
Daniel Dougherty
Amyris (NASDAQ: AMRS) is a science and technology leader in the research, development and production of pure, sustainable ingredients for the Health & Wellness, Clean Beauty and Flavors & Fragrances markets. Amyris applies its exclusive, advanced technology, including state-of-the-art machine learning, robotics and artificial intelligence to engineer yeast, that when combined with sugarcane syrup through fermentation, is converted to highly pure molecules for specialty ingredients. Amyris manufactures sustainably-sourced ingredients at industrial scale for B2B partners and further distribution to over 3,000 of the world's top brands, reaching more than 200 million consumers. Amyris stands by its No Compromise® promise that everything it makes is better for people and the planet. In this presentation, we provide examples of computational techniques used throughout the design, build, test, and learn phases of research and development. We’ll highlight prominent aspects of the natural biology of yeast and how they inform the computational approaches used. Measures of statistical and computational efficiency will be provided and we’ll conclude with some recommendations for future developments.
-
Judy Day
From work initiated at the Mathematical Biosciences Institute, a mathematical model was published in 2011 that investigated the immune response to inhalation anthrax infection. That publication led to a collaboration with the U.S. Environmental Protection Agency which blossomed into a Investigative Working Group effort supported by the National Institute for Mathematical and Biological Synthesis. This group included experts from both the anthrax research community as well as mathematical modelers. Over a period of several years, members of this group explored the utility of mathematical modeling in understanding risk in low dose inhalation anthrax infection. This poster describes the journey of the research that was inspired by these events and discusses the results and relationships it generated.
-
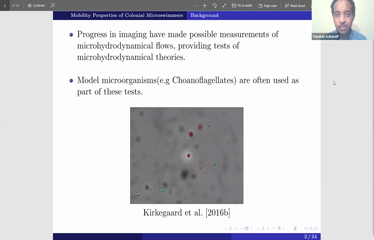
Yonatan Ashenafi
We study the stochastic hydrodynamics of aggregate random walkers (ARWs) typified by organisms called Choanoflagellates. The objective is to link cell-scale dynamics to colony-scale dynamics for Choanoflagellate rosettes and chains. We use a synthesis of linear autoregressive stochastic processes to explain the effective statistical dynamics of the Choanoflagellate colonies in terms of colony parameters. We model and characterize the non-linear chemotactic reaction of the aggregates to a local chemical gradient in terms of colony parameters.
-
Alessandro Maria Selvitella
Authors:
Prof. Kathleen Lois Foster, Department of Biology, Ball State University
Prof. Alessandro Maria Selvitella, Department of Mathematical Sciences, Purdue University Fort Wayne
Extraordinary advancements in computing power have facilitated the development and application of sophisticated statistical analyses to biological fields such as genomics, ecology, and evolution. However, even now, when powerful hardware and software tools have never been more accessible and despite significant advancements in statistical theory, physiological branches of biology, like biomechanics, seem to be stuck in the past, with the ubiquitous and almost exclusive use of classical univariate statistics. In this poster, we will discuss how more modern machine learning methods impact and revolutionize the extraction and analysis of biomechanical data. This will be discussed in the context of lizard locomotion and contrasted with the results of classical univariate analyses.
-
Shuying Sun
Authors:
Shuying Sun, Sherwin Massoudian, and Allison Bertie Johnson
Haplotype information is important to further understand the genetic processes of diseases. Therefore, it is crucial to obtain haplotypes for disease studies. With the development of next generation sequencing (NGS) technologies, it is now possible to obtain haplotypes using sequencing reads. The process of determining haplotypes based on sequencing reads is called haplotype assembly. It is challenging to conduct haplotype assembly because NGS datasets are very large and have complex genetic and technological features. Even though a large number of approaches or software packages have been developed, it is unclear how well these programs perform. Most of them are not well evaluated as they may be only compared with a small number (e.g., 1 or 2) of other methods and are validated based on different datasets. In this project, we conduct a comprehensive analysis to compare a few currently available haplotype assembly software packages. We will assess them based on their statistical or computational methods, algorithmic components, and evaluation features as well. We will show our comparison results based on a publicly available dataset. With our comparison results, we shall provide users with both detailed input on the performance of current methods and new perspectives on haplotype assembly, which will be helpful for developing more accurate and efficient algorithms.
-
Veronica Ciocanel
Contractile rings are cellular structures made of actin filaments that are important in development, wound healing, and cell division. In the reproductive system of the roundworm C. elegans, ring channels allow nutrient exchange between developing egg cells and the worm and are regulated by forces exerted by myosin motor proteins.
In this work, we use an agent-based modeling and data analysis framework for the interactions between actin filaments and myosin motor proteins inside cells. This approach may provide key insights for the mechanistic differences between two motors that are believed to maintain the rings at a constant diameter. In particular, we propose tools from topological data analysis to understand time-series data of filamentous network interactions. Our proposed methods clearly reveal the impact of certain parameters on significant topological circle formation, thus giving insight into ring channel formation and maintenance.
-
Jeff Gaither
Recent years have seen an explosion in the use of machine-learning algorithms to classify human mutations. There are now at least 30 scores designed to identify mutations likely to be deleterious to humans, but almost all are "black boxes" that provide no explanation of how they arrived at their predictions. In this talk I'll introduce a new mutational pathogenicity score, SNPDogg, that is transparent, insofar as every prediction can be decomposed as a sum of contributions from the model's features. SNPDogg's feature-importance ​values are computed via a game-theoretic approach implemented in the "shap" python package.
-
Alla Borisyuk
Astrocytes are glial cells making up 50% of brain volume, and playing multiple important roles, e.g. control of synaptic transmission. We are developing tools to include “effective� astrocytes in neuronal network models in an easy-to-implement, and relatively computationally-efficient way. In our approach we first consider neuron-astrocyte interaction at fine spatial scale, and then extract essential ways in which the network is influenced by the presence of the astrocytes.
For example, the tightness of astrocyte wrapping (or “degree of ensheathement�) and the number of the synapses ensheathed varies by brain region and in certain disease states such as some forms of epilepsy. Do the changes in ensheathment properties contribute to the diseased state of the network or, conversely, play a protective role?
To address this question, first, we consider an individual synapse as a DiRT (Diffusion with Recharging Traps) model: diffusing particles can escape through absorbing parts of the boundary, or can be captured by traps on the boundary. We show that a synapse tightly ensheathed by an astrosyte makes neuronal connection faster, weaker, and less reliable. These influences can then be included in a neuronal network model by adding a simplified “effective� astrocyte on each synapse. We find that depending on the number of synapses ensheathed, and the ensheathment strength, the astrocytes are able to push the network to synchrony and to exhibiting strong spatial patterns, possibly contributing to epileptic disorder.
-
Alexandria Volkening
Agent-based dynamics appear across the natural and social world; applications include swarming and flocking, pedestrian crowd movement, and self-organization of cells during the early development of organisms. Though disparate in application, many of these emergent patterns and collective dynamics share similar features (e.g. long-range communication, noise, fluctuations in population size, and multiple types of agents) and face some of the same modeling and analysis challenges. In this talk, I will focus on the example of pigment-cell interactions during zebrafish-pattern formation to illustrate various ways of modeling agent behavior. We will discuss how agent-based models are related to other approaches (e.g., cellular automaton and continuum models) and highlight methods for analyzing cell-based dynamics using topological techniques.
-
Duan Chen
Our recent work is motivated by two types of biological problems. One is inferring 3D structures of chromatins based on chromosome conformation capture (3C), such as Hi-C, which is a high-throughput sequencing technique that produces millions of contact data between genomic loci pairs. The other problem is computational deconvolution of gene expression data from heterogeneous brain samples, for extracting cell type-specific information for patients with Alzheimer's Disease (AD). Both problems involve large volumes of data, thus fast algorithms are indispensable in either direct optimization or machine learning methods. A central approach is the low-rank approximation of matrices. Conventional matrix decomposition methods such as SVD, QR, etc, are expensive, so not suitable for repeated implementation in these biological problems. Instead, we develop fast stochastic matrix compressions based on randomized numerical linear algebra (RNLA) theories. In this talk, we will emphasize on a recently developed stochastic kernel matrix compression algorithm. In this algorithm, samples are taken at no (or low) cost and the original kernel matrix is reconstructed efficiently with desired accuracy. Storage and compressing processes are only at O(N) or O(NlogN) complexity. These stochastic matrix compressing can be used to the above-mentioned biological problems to greatly improve algorithm efficiency, they can also be applied to other kernel based machine learning algorithms for scientific computing problems with non-local interactions (such as fractional differential equations), since no analytic formulation of the kernel function is required in our algorithms.
-
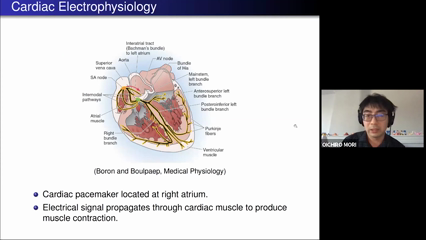
Yochiro Mori
The bidomain model is the standard model describing electrical activity of the heart. We discuss the stability of planar front solutions of the bidomain equation with a bistable nonlinearity (the bidomain Allen�Cahn equation) in two spatial dimensions. In the bidomain Allen�Cahn equation a Fourier multiplier operator whose symbol is a positive homogeneous rational function of degree two (the bidomain operator) takes the place of the Laplacian in the classical Allen�Cahn equation. Stability of the planar front may depend on the direction of propagation given the anisotropic nature of the bidomain operator. We establish various criteria for stability and instability of the planar front in each direction of propagation. Our analysis reveals that planar fronts can be unstable in the bidomain Allen�Cahn equation in striking contrast to the classical or anisotropic Allen�Cahn equations. We identify two types of instabilities, one with respect to long�wavelength perturbations, the other with respect to medium�wavelength perturbations. Interestingly, whether the front is stable or unstable under long�wavelength perturbations does not depend on the bistable nonlinearity and is fully determined by the convexity properties of a suitably defined Frank diagram. On the other hand, stability under intermediate�wavelength perturbations does depend on the choice of bistable nonlinearity. Intermediate�wavelength instabilities can occur even when the Frank diagram is convex, so long as the bidomain operator does not reduce to the Laplacian. We shall also give a remarkable example in which the planar front is unstable in all directions. Time permitting, I will also discuss properties of the bidomain FitzHugh Nagumo equations. This is joint work with Hiroshi Matano, Mitsunori Nara and Koya Sakakibara.
-
Adrian Lam
Beginning with the work of Alan Hastings in 1983, PDE models have played a major role in the mathematical study of evolution of dispersal. In this talk, I will discuss two classes of PDE models that comes from evolution of dispersal. In the first part, I will discuss existence/non-existence of evolutionarily stable strategies (ESS) in two-species competition models, which is motivated by the adaptive dynamics approach. In the second part, I will introduce a new class of models that describes a population structured by a quantitative trait, which describes the competition of an infinite number of species in a certain sense. We show the convergence to ESS in these models of a quantitative trait, and explain how that is connected to the aforementioned adaptive dynamics framework. This talk contains projects in collaboration with R.S. Cantrell, C. Cosner, M. Golubitsky, W. Hao, B. Perthame, Y. Lou, and F. Lutscher.
-
German Enciso
In this work, we provide a systematic control of a given biochemical reaction network through a control module reacting with the existing network system. This control module is designed to confer so-called absolute concentration robustness (ACR) to a target species in the controlled network system. We show that when the deterministic network system is controlled with the ACR controller, the concentration of a species of interest has a steady state at the desired value for any initial amounts, and it converges to the value under some mild conditions. For the stochastic counterparts of reaction network systems, we further show that when the abundance of the control species is high enough, the ACR controller can be utilized to make a target species approximately follow a Poisson distribution centered at the desired value. For this framework, we use the deficiency zero theorem (Anderson et al, 2010) in chemical reaction network theory and multiscaling model reduction methods. This control module also brings robust perfect adaptation, which is a highly desirable goal of the control theory, to the target species against transient perturbations and uncertainties in the model parameters.
-
Martin Wechselberger
In this talk I will review geometric singular perturbation theory, but with a twist— I focus on a coordinate-independent setup of the theory. The need for such a theory beyond the standard form is motivated by looking at biochemical reaction, electronic and mechanical oscillator models that show relaxation-type behaviour. While the corresponding models incorporate slow and fast processes leading to multiple time-scale dynamics, not all of these models take globally the form of a standard slow–fast system. Thus from an application point of view, it is desirable to provide tools to analyse singularly perturbed systems in a coordinate-independent manner.
-
Casey Diekman
Modern data assimilation (DA) techniques are widely used in climate science and weather prediction but have only recently begun to be applied in neuroscience. In this talk I will illustrate the use of DA algorithms to estimate unobserved variables and unknown parameters of conductance-based neuronal models and propose the bifurcation structure of inferred models as a qualitative measure of estimation success. I will then apply DA to electrophysiological recordings from suprachiasmatic nucleus neurons to develop models that provide insight into the functioning of the mammalian circadian clock. Finally, I will frame the selection of stimulus waveforms to inject into neurons during patch-clamp recordings as an optimal experimental design problem and present preliminary results on the optimal stimulus waveforms for improving the identifiability of parameters for a Hodgkin-Huxley-type model.
-
Daniel Forger
Millions of Americans track their steps, heart rate, and other physiological signals through wearables. The scale of this data is unprecedented; I will describe several of our ongoing studies each of which collects wearable and mobile data from thousands of users, even in > 100 countries. This data is so noisy that it often seems unusable. It is in desperate need of new mathematical techniques to extract key signals that can be used in the (ode) mathematical modeling typically done in mathematical biology. I will describe several techniques we have developed to analyze this data and simulate models including gap orthogonalized least squares, a new ansatz for coupled oscillators which is similar to the popular ansatz by Ott and Antonsen, but which gives better fits to biological data and a new level-set Kalman Filter that can be used to simulate population densities. I will also describe how these methods can be used to understand the impact of social distancing and COVID lockdowns on circadian timekeeping and sleep.
-
Juan B. Gutierrez
Authors:
Jacob B Aguilar, PhD, Saint Leo University.
Jeremy Samuel Faust, MD, Brigham and Women's Hospital
Lauren M. Westafer, MD, University of Massachusetts, Medical School-Baystate
Juan B. Gutierrez, PhD, University of Texas at San Antonio
It is during critical times when mathematics can shine and provide an unexpected answer. Coronavirus disease 2019 (COVID-19) is a novel human respiratory disease caused by the SARS-CoV-2 virus. Asymptomatic carriers of the virus display no clinical symptoms but are known to be contagious. Recent evidence reveals that this sub-population, as well as persons with mild, represent a major contributor in the propagation of COVID-19. The asymptomatic sub-population frequently escapes detection by public health surveillance systems. Because of this, the currently accepted estimates of the basic reproduction number (Ro) of the virus are too low. In this talk, we present a traditional compartmentalized mathematical model taking into account asymptomatic carriers, and compute Ro exactly. Our results indicate that an initial value of the effective reproduction number could range from 5.5 to 25.4, with a point estimate of 15.4, assuming mean parameters. It is unlikely that a pathogen can blanket the planet in three months with an Ro in the vicinity of 3, as reported in the literature; in fact, no other plausible explanation has been offered for the rapid profession of this disease. This model was used to estimate the number of cases in every county in the USA.
-
Jae Kyoung Kim
Despite dramatic advances in experimental techniques, many facets of intracellular dynamics remain hidden, or can be measured only indirectly. In this talk, I will describe three strategies to analyze timeseries data from biological systems with hidden parts: replacement of hidden components with either time delay, quasi-steady-state or random regulatory process. Then, I will illustrate how the simplification with the time delay can be used to understand the processes of protein synthesis, which involves multiple steps such as transcription, translation, folding and maturation, but typically whose intermediates proteins cannot be measured. Furthermore, I will illustrate how the simplification with the quasi-steady-state can be used to develop an accurate method to estimate drug clearance, which occurs in multiple steps of metabolism, which greatly improved the canonical approach used in more than 65,000 published papers for last 30 years. Finally, I will describe a systematic modeling selection approach to identify hidden regulatory biochemical connections leading to the observed timeseries data. Then, I will illustrate how we applied the approach to find the connection between the circadian clock and cell cycle checkpoints.
-
David Rand
Recent research has shown that the circadian clock has a much more profound effect on human health than previously thought. I will present a machine-learning approach to measuring circadian clock functionality from the expression levels of key genes in a single tissue sample and then apply this to study survival in a breast cancer clinical trail.
A principal aim of circadian medicine is to develop techniques and methods to integrate the relevance of biological time into clinical practice. However, it is difficult to monitor the functional state of the circadian clock and its downstream targets in humans. Consequently, there is a critical need for tools to do this that are practical in a clinical context and our approach tackles this. We apply our algorithm to breast cancer and show that in a large cohort of patients with non-metastatic breast cancer the resulting dysfunction metric is a prognostic factor for survival providing evidence that it is independent of other known factors. While previous work in this area is focused on individual genes, our approach directly assesses the systemic functionality of a key regulatory system, the circadian clock, from one sample.
-
Jay Newby
Despite being one of the fundamental cell structures, we know surprisingly little about the cytosol. Its physical properties are difficult to measure due to technical challenges: the means of spatially resolving viscosity, elasticity, flow, crowding, and confinement within cells that fluctuate and grow. Changes in macromolecular crowding can directly influence protein diffusion, reaction rates, and phase separation. I will discuss new particle tracking tools and how we use them to quantitatively measure the physical state of the cytosol by studying the three-dimensional stochastic motion of genetically expressed fluorescent nanoparticles (GEMs). Using these particle probes, we find that the physical properties of the cytosol vary significantly within and between cells, indicating that the fundamental state of the cytosol is a key source of heterogeneity within genetically identical cells.
-
Sean Lawley
Why do 300 million sperm cells search for the oocyte in human fertilization when only a single sperm cell is necessary? Why do 1000 calcium ions enter a dendritic spine when only two ions are necessary to activate the relevant Ryanodine receptors? The seeming redundancy in these and many other biological systems can be understood in terms of extreme first passage time (FPT) theory.
While FPT theory is often used to estimate timescales in biology, the overwhelming majority of studies focus on the time it takes a given single searcher to find a target. However, in many scenarios the more relevant timescale is the FPT of the first searcher to find a target from a large group of searchers. This so-called extreme FPT depends on rare events and is often orders of magnitude faster than the FPT of a given single searcher. In this talk, we will explain recent results in extreme FPT theory and show how they modify traditional notions of diffusion timescales.
-
Sam Isaacson
For a chemical signal to propagate across a cell, it must navigate a tortuous environment involving a variety of organelle barriers. In this work we study mathematical models for a basic chemical signal, the arrival times at the nuclear membrane of proteins that are activated at the cell membrane and diffuse throughout the cytosol. Organelle surfaces within human B cells are reconstructed from soft X-ray tomographic images, and modeled as reflecting barriers to the molecules’ diffusion. We show that signal inactivation sharpens signals, reducing variability in the arrival time at the nuclear membrane. Inactivation can also compensate for an observed slowdown in signal propagation induced by the presence of organelle barriers, leading to arrival times at the nuclear membrane that are comparable to models in which the cytosol is treated as an open, empty region. In the limit of strong signal inactivation this is achieved by filtering out molecules that traverse non-geodesic paths.
-
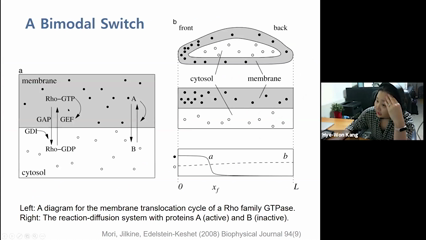
Hye-Won Kang
A sequence of metabolic enzymes tightly regulates glycolysis and gluconeogenesis. It has been hypothesized that these enzymes form multienzyme complexes and regulate glucose flux. In the previous work, it was identified that several rate-limiting enzymes form multienzyme complexes and control the direction of glucose flux between energy metabolism and building block biosynthesis. A recent study introduced a mathematical model to support this finding, in which the association of the rate-limiting enzymes into multienzyme complexes in included. However, this model did not fully account for dynamic and random movement of the enzyme clusters, as observed in the experiment.
In this talk, I will introduce a stochastic model for enzyme clustering in glucose metabolism. The model will describe both the enzyme kinetics and the spatial organization of metabolic enzyme complexes. Then, I will discuss underlying model assumptions and approximation methods.
-
Yangjin Kim
Tumor cells interact with many players such as stromal cells (fibroblasts, myofibroblasts), immune cells (N1/N2 neutrophils, M1/M2 macrophages, NK cells, T cells), and extracellular matrix (ECM) in a tumor microenvironment in order to increase survival rates in response to multiple biomechanical and biochemical challenges. Quite often, these tumor cells exchange major regulatory molecules with other cells and use intracellular signaling pathways for regulation of cellular decision such as cell motility, proliferation, apoptosis, and necroptosis after receptor binding. For example, stem cells-like astrocytes and M1/M2 microglia communicate with glioma cells for regulation of tumor growth and cellular dispersion after surgical resection of the primary tumorcore, and one of major ECM components in brain, CSPG, was shown to play a key role in regulation of anchoring invasive glioma cells. We developed hybrid multi-scale models of cancer dynamics where intracellular components (ODEs), diffusible molecules (PDEs), and individual cells are integrated in the hybrid domain. We show how up- or down-regulation of components in these pathways in cancer cells affects the key cellular decision to infiltrate or proliferate by interacting with many players in a complex microenvironment. We take some examples in glioblastoma (brain cancer) before and after surgery, breast cancer, and metastatic circulating tumor cells (CTC).
-
Tie-Jun Li
Detecting the change of biological interaction networks is of great importance in biological and medical research. We proposed a simple loss function, named as CrossFDTL, to identify the network change or differential network by estimating the difference between two precision ma- trices under Gaussian assumption. The CrossFDTL is a natural fusion of the D-trace loss for the considered two networks by imposing the l1 penalty to the differential matrix to ensure sparsity. The key point of our method is to utilize the cross variables, which correspond to the sum and difference of two precision matrices instead of using their original forms. Moreover, we developed an efficient minimization algorithm for the proposed loss function and further rigorously proved its convergence. Numerical results showed that our method outperforms the existing methods in both accuracy and convergence speed for the simulated and real data.
